중2 수학 직각삼각형 닮음 기본문제와 중점 나오는 2가지 유형

수학공부 초등중등수학

JeromeEugeneMorrow 2024. 12. 3. 18:20

중2 수학 닮음 문제에서 가장 많이 나오는 것이 직각 삼각형의 닮음 문제에요.

닮음이 뭔지 안다는 걸 일단 전제로 할게요. 닮음 문제는 기본적으로 비례 문제에요.

그럼 뭐가 뭐랑 비례인지를 찾으면 되요. 직각 삼각형에서 2가지 문제가 있어요. 하나는 직각 삼각형을 긴 편이 바닥을 향하게 놓고 윗 꼭지점에서 아래로 내려서 직각 삼각형을 2개로 쪼갠 후 비율 구하는 문제에요.

이 3가기 중에 모든 문제가 있어요. 그러니까 1번은 8의 제곱은 6x )(6+x) 가 되는거구요.

2번은 6의 제곱은 3x (x+3)가 된다는거에요. 쉽죠?

3번은 3의 제곱은 x곱하기 4가 되고요. 쉽죠? 네 이게 기본이에요. 직각삼각형 닮음 문제는 다 이 범위 안에 있어요.

자 이제 좀 어려운것은 중점이 나오는 문제에요.

직각 삼각형에 뜬근없이 삼각형 하나를 더 집어 넣어요. 이런 모양을 만드는거에요. 그런데 이건 A와 M까지 거리를 물어보는 경우가 대부분 문제에요. 그런데 이건 잘 AM을 원의 반지름이라고 생각하면 되요. 이게 왜 그런거냐..

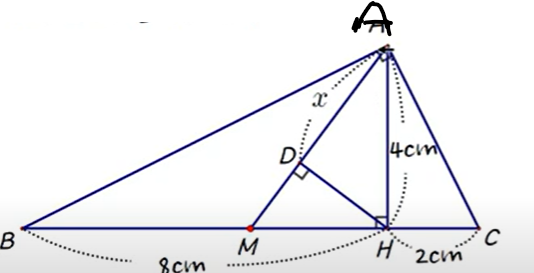
직각삼각형의 빗변의 중점은 직각삼각형의 외심 그러니까 삼각형 세 점을 잇는 큰 동그라미를 그리면 그걸 외접원이라고 하고 그 중심이라는거에요. 기억나죠? 직각삼각형은 외심이 항상 저 빗변 가운데 있어요. 그러면 그림에서 BM과 MC는 큰 동그라미의 반지름이에요.

그러니까.. AH의 제곱은 ad와 am을 곱한것이 되는거에요. 그런데 MD는 x 이고 MM은 5지요.. 반지름이니까요.. 10의 반.. 이제 구할 수 있겠지요?

위 설명 내용은 아래 영상에서 잘 설명하신 선생님의 것을 참고한 것입니다.

자 그러면 아래 2개의 문제도 쉽게 풀수 있을거에요.

자 이 문제는 x 를 먼저 구해야 하죠? 그러니까 13의 제곱은 12 x (12+x) 그러니까 12(x+1) 은 13의 2 제곱이고..

13의 제곱은 169 에서 144 + 12x 그러니까 x는 25/12

그 다음 y, 구할 차례 y는 닮음의 비례를 이용해서 빗변 대 높이 13:12 = y : 5 그러니까.. 12y = 65 그러니까 y는 65/12

그래서 x더하기 y 는 25/12 + 65 /12 = 90 / 12 = 15 / 2 입니다.

두번째 문제

자 M이 중점이에요. 그러니까 bm과 am은 반지름이죠.. 외접원의 그러니까 반지름은 5군요. 자 그럼 닮은 삼각형은 가장 바깥 큰 삼각형 aABC 이고 DAM이 닮은 삼각형..

그러니까 AD의 제곱은 8x2 = 16 그러니까 AD는 4 군요.

그럼 이제 삼각형 AMD를 생각해봐요 방금 구한 4의 제곱은 AE 곱하기 AM 이죠. 그런데 AM이 반지름이니까 5에요.

그러면 16= AE X 5 따라서 AE는 16/ 5군요.